In this article, we will consider key concepts of discriminative and generative models, differences between them. In the light of these concepts, we will describe logistic regression, Naive Bayes classifier and differentiable generator nets.

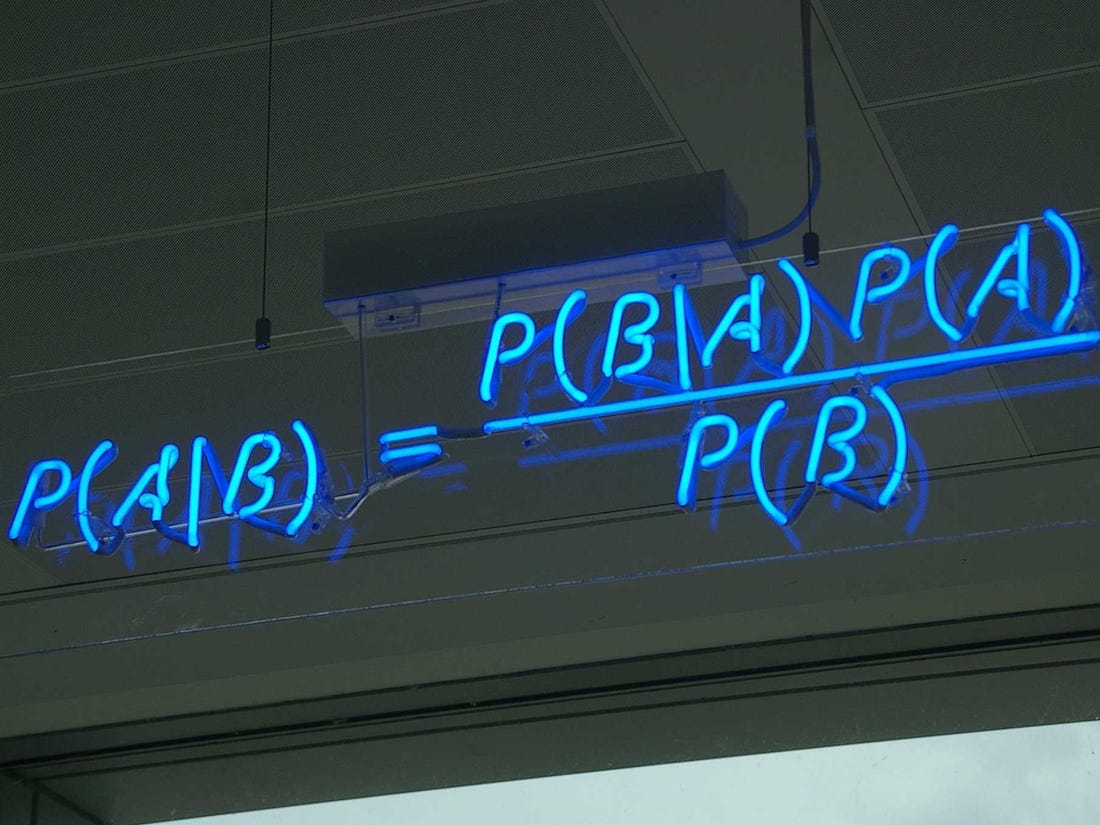
Discriminative models train function \(f:\mathbf{x} \to y\), which map input vector \(\mathbf{x}\) to some label \(y\). In probabilistic point of view it means that we learning conditional distribution \(p(y \vert \mathbf{x})\). And this approach can be represented by the following methods:

• k-nearest neighbors algorithm;
• Logistic regression;
• Support vector machine (SVM);
• Maximum-entropy Markov models;
• Conditional random fields;
• Neural networks.

In the case of discriminative approach training dataset look like: \(D=\{(\mathbf{x}^{(i)}; y_i) \vert i < N \in \mathbb{Z}\}\), here \(\mathbf{x}^{(i)}\) is a sample from feature matrix space \(\mathbf{X}\) and \(y_i\) is corresponding label from \(\mathbf{Y}\). As usual in machine learning task, we have to find optimal weights. For discriminative model we try to find maximum likelihood estimation (MLE)

\[\boldsymbol{\hat{\theta}} = \underset{\boldsymbol{\theta}}{\operatorname{arg max}} \, p(\mathbf{Y} \vert \mathbf{X}; \, \boldsymbol{\theta})\]

If we assume that all the examples are independent and equally distributed, then this expression can be represented as follows

\[\boldsymbol{\hat{\theta}} = \underset{\boldsymbol{\theta}}{\operatorname{arg max}} \, \sum_{i=1}^N \, \log{p} (y_i \vert \mathbf{x}^{(i)}; \, \boldsymbol{\theta})\]

MLE method helps us to get optimal loss-function expression from different probabilistic distributions. Let’s illustrate this fact with an example of binary cross entropy loss-function derivation. For example, we have conducted \(\mathit{N}\) experiments with a coin, we have tossed a coin \(\mathit{N}\) times and \(\mathit{n}\) times we got head. What is the probobility to obtain heads in experiments \(\mathit{p}(heads)\)?
Here we have a probability space with two possible outcomes: head and tail. After provided experiments there will be finite sequence of independent random variables \(\mathit{X_1}, \dots, \mathit{X_m}\), for each \(i=1,\dots ,m\), random variable \(\mathit{X_i}\) will take the head value with probability \(\mathit{p}\) and tail value with probability \(1 - \mathit{p}\). To model probabilities in such kind of tasks Binomial distribution fits well, thus we have,

\[\mathit{P}(n) = C_{N}^n \, p^n \, (1-p)^{N-n}\] \[C_{N}^n = \frac{N!}{n!(N-n)!}\]

MLE estimation written as follows

\[\begin{array}{cc} \underset{\mathit{p}}{\operatorname{arg max}} \, P(n) = \underset{\mathit{p}}{\operatorname{arg max}} \, \log{P(n)} = \\ = \underset{\mathit{p}}{\operatorname{arg max}} \, \lbrack \log{C_{N}^n} + n\,\log{p} + (N-n)\log{(1-p)} \rbrack = \\ = \underset{\mathit{p}}{\operatorname{arg max}} \, \lbrack \displaystyle \frac{n}{N}\log{p} + (1 - \frac{n}{N})\log{(1-p)} \rbrack = \\ = \underset{\mathit{p}}{\operatorname{arg max}} \, \lbrack \tilde{p}\log{p} + (1 - \tilde{p})\log{(1-p)} \rbrack \end{array}\]

Here \(\tilde{p}\) is a target and \(\mathit{p}\) is a value we want to adjust. Then if we find the partial derivative of \(\mathit{f}\) with respect to the parameter \(\mathit{p}\), equate it to zero and solve it with respect to \(\mathit{p}\), we found out that optimal value which maximize this equation will be \(\mathit{p} = \displaystyle \frac{n}{N}\).
Since usually in machine learning tasks we need to minimize some differentiable function, we rewrite the equation above in the following form

\[\underset{p}{\operatorname{arg min}} \, \lbrack - \tilde{p}\log{p} - (1 - \tilde{p})\log{(1-p)} \rbrack\]

As a result, in parentheses we can see the familiar binary cross entropy function, which is used in binary classification problem using logistic regression.

Generative models train joint probability distribution \(\mathit{p}(\mathbf{x}, y)\), and it can be used to get conditional distribution \(p(y \vert \mathbf{x})\) using the Bayes’s theorem, because if we fix \(\mathbf{x}\), we will get \(p(y \vert \mathbf{x}) = {\displaystyle \frac{p(\mathbf{x}, y)}{p(\mathbf{x})} \propto p(\mathbf{x}, y)}\). The joint probabilistic distribution gives more information and we can use it to generate new data. Below are examples of generative methods:

• Gaussian mixture model;
• Hidden Markov model;
• Bayesian network (e.g. Naive bayes, Autoregressive model);
• Latent Dirichlet allocation;
• Boltzmann machine (e.g. Restricted Boltzmann machine, Deep belief network);
• Variational autoencoder;
• Generative adversarial network.

The main goal of the generative model is as follows: for training dataset \(\mathit{D}=\{\mathbf{x}^{(i)} \vert i < \mathit{N} \in \mathbb{Z}\}\) maximize \(\prod_{i=1}^N \, p(\mathbf{x}^{(i)}; \boldsymbol{\theta})\) over \(\boldsymbol{\theta}\), so this equivalent to

\[\boldsymbol{\hat{\theta}} = \underset{\boldsymbol{\theta}}{\operatorname{arg max}} \, \sum_{i=1}^N \, \log{p}( \mathbf{x}^{(i)}; \, \boldsymbol{\theta})\]

One way to interpret MLE estimation is to consider it as minimizing the Kullback–Leibler divergence between the empirical distribution \(p_{data}\) represented by training set, and distribution \(p\), which is obtained from our model. The Kullback – Leibler divergence is determined by the formula

\[KL(p_{data}(\mathbf{X}), p(\mathbf{X}, \boldsymbol{\theta})) = \int p_{data}(\mathbf{X}) \log{p(\mathbf{X}, \boldsymbol{\theta})}dX = \sum_{i=1}^N p_{data}(\mathbf{x}^{(i)}) \log{p(\mathbf{x}^{(i)}, \boldsymbol{\theta})}\]

and minimization of this expression is equivalent to maximization of likelihood. In generative models, the probability density function (PDF) can be expressed, either explicitly or implicitly. In the case of an explicit PDF, probabilistic assumptions are made, which usually come down to the fact that the total distribution is expressed as the product of other distributions. As an example, we can consider Naive Bayes algorithm. This method estimates conditional propability \(\mathit{p}(y \vert \mathbf{x})\) from joint probability

\[p(\mathbf{x}, y) = p(\mathbf{x} \vert y)p(y) = p(x_1, \dots, x_N \vert y)p(y) = p(y)\prod_{i=1}^N p(x_i \vert y)\]

where \(y\) is some label, and \(\mathbf{x}\) is input sequence. Thus, algorithm makes the explicit assumption that each \(x_i\) is conditionally independent of each of the other \(x_k\) given label \(y\). The fundamental equation for the Naive Bayes classifier will look as follows

\[p(y \vert x_1, \dots, x_N) = \frac{p(y) \prod_{i} p(x_i \vert y)}{\sum_{j} p(y_j) \prod_{i} p(x_i \vert y_j)}\]

Among another class of generative models with an implicit PDF, differentiable generator nets are widespread, it includes widely used Generative Adversarial Networks (GAN) represented by generator and discriminator networks. Differentiable generator networks are used to generate samples directly without any probabilistic assumptions, in the case of GAN we’re training neural network to represent a parametric family of nonlinear functions \(g\) and, using training data, we derive parameters that can help to select the desired function.
In other words, some differentiable generator transforms examples of latent variables \(\mathbf{z}\) into examples \(\mathbf{x}\) using a differentiable function \(g(\mathbf{z}; \boldsymbol{\theta}^{(g)})\), which represented by neural network. For example, we take samples from normal distribution with zero mean and identity covariance matrix \(\mathbf{z} \sim N(0, \mathbf{I})\) and want to get samples \(\mathbf{x} \sim N(\mu, \mathbf{\Sigma})\), which is normally distributed with mean \(\mu\) and covariance matrix \(\mathbf{\Sigma}\). We can apply to \(\mathbf{z}\), simple generative network with one affine layer

\[\mathbf{x} = g(\mathbf{z}) = \mu + \mathbf{L}\mathbf{z}\]

where \(\mathbf{L}\) is determined by the Cholesky decomposition of the matrix \(\mathbf{\Sigma}\).
We can assume that \(g\) defines a nonlinear change of variables that transforms the distribution of \(\mathbf{z}\) into the desired distribution of \(\mathbf{x}\). For reversible differentiable continuous function \(g\) identity holds

\[p_{z}(\mathbf{z}) = p_{x}(g(\mathbf{z})) \, \lvert \det(\frac{\partial{g}}{\partial{\mathbf{z}}}) \rvert\]

Thus, we implicitly determine the probability distribution of \(\mathbf{x}\)

\[p_{x}(\mathbf{x}) = \frac{p_{z}(g^{-1}(\mathbf{x}))}{\lvert \det(\frac{\partial{g}}{\partial{\mathbf{z}}}) \rvert}\]

Of course, for some \(g\), this expression is difficult to calculate, so we often use indirect training methods for \(g\), instead of trying to maximize \(\log{p(\mathbf{x})}\) directly.

Summary

• the main difference between discriminative model and generative one is that the conditional probability distribution \(p(y \vert \mathbf{x})\) in the case of the discriminant model is estimated directly from the data. In the case of generative model, to obtain a conditional probability distribution \(p(y \vert \mathbf{x})\), the joint probability distribution \(p(\mathbf{x}, y)\) need to be estimated first;
• discriminative models may include those which are not based on a probabilistic approach, for example, SVM method or neural networks;
• generative models are more complex and they allow to solve not only the classification problem, but also generate new data samples which are similar to samples from a training dataset.